Золотий перетин

Наша взаимовыгодная связь https://banwar.org/

"Золотий перетин"

Реферат виконала: учениця 8 класу МОУ гімназія №9 Вьюшіна Вероніка

Єкатеринбург

2002

1. Введення. Пропорція золотого перетину. Ф і φ.

"Геометрія володіє двома великими скарбами. Перше - це теорема Піфагора, друге - ділення відрізка в крайньому і середньому відношенні"

Йоганн Кеплер

Правильні багатокутники привертали увагу давньогрецьких вчених ще задовго да Архімеда. Піфагорійці, що вибрали емблемою свого союзу пентаграму - п'ятикутну зірку, надавали дуже велике значення задачі про розподіл кола на рівні частини, тобто про побудову правильного вписаного багатокутника. Альбрехт Дюрер (1471-1527гг), який став уособленням Відродження в Німеччині призводить теоретично точний спосіб побудови правильного п'ятикутника, запозичений з великого твору Птолемея "Альмагест".

Інтерес Дюрера до побудови правильних багатокутників відображає використання їх в середні віки в арабських і готичних орнаментах, а після винаходу вогнепальної зброї - в плануванні фортець.

Середньовічні способи побудови правильних багатокутників носили наближений характер, але були (або не могли не бути) простими: перевага віддавалася способам побудови, що не вимагає навіть змінювати розчин циркуля. Леонардо да Вінчі також багато писав про багатокутники, але саме Дюрер, а не Леонардо, передав середньовічні способи побудови нащадкам. Дюрер, звичайно, був знайомий з "Началами" Евкліда, але не навів у своєму "Керівництві до вимірювання" (про побудовах за допомогою циркуля і лінійки) запропонований Евклідом спосіб побудови правильного п'ятикутника, теоретично точний, як і всі евклідові побудови. Евклід не намагається розділити задану дугу окружності на три рівні частини, і Дюрер знав, хоча доказ було знайдено лише в XIX столітті, що ця задача нерозв'язна.

Запропоноване Евклидом побудова правильного п'ятикутника включає в себе розподіл відрізка прямої в середньому і крайньому відношенні, назване згодом золотим перетином і привертає до себе увагу художників і архітекторів протягом декількох століть.

Точка В ділить відрізок АВЕ в середньому і крайньому відношенні або утворює золотий перетин, якщо відношення більшої частини відрізка до меншої дорівнює відношенню всього відрізка до більшої частини.

Записане у вигляді рівності відносин золотий перетин має вигляд

АВ / ВЕ = АВ / АЕ

Якщо покласти АВ = а, а ВЕ = а / Ф так, щоб золоте відношення дорівнювало АВ / ВЕ = Ф, то виходить співвідношення

Ф = 1 + 1 / Ф

Тобто Ф задовольняє рівнянню

Ф2 Ф-1 = 0

Це рівняння має один позитивний корінь

Ф = (√5 + 1) /2=1.618034....

Зауважимо, що 1 / Ф = (√5 -1) / 2, так як (√5-1) (√5 + 1) = 5-1 = 4. За 1 / Ф прийнято вважати φ = 0.618034 ....

Ф і φ - прописна і рядкова форми грецької букви "фе".

Таке позначення прийнято на честь давньогрецького скульптора Фідія (V століття до н. Е.) Фідій керував будівництвом храму Парфенон в Афінах. В пропорціях цього храму багаторазово присутній число φ.

2.История золотого перетину

Прийнято вважати, що поняття про золотий розподіл увів у науковий обіг Піфагор, давньогрецький філософ і математик (VI ст. До н.е.). Є припущення, що Піфагор своє знання золотого розподілу запозичив у єгиптян і вавилонян. І дійсно, пропорції піраміди Хеопса, храмів, барельєфів, предметів побуту і прикрас з гробниці Тутанхамона свідчать, що єгипетські майстри користувалися співвідношеннями золотого розподілу при їхньому створенні. Французький архітектор Ле Корбюзьє знайшов, що в рельєфі з храму фараона Сеті I в Абідосі і в рельєфі, що зображує фараона Рамзеса, пропорції фігур відповідають величинам золотого розподілу. Зодчий Хесира, зображений на рельєфі дерев'яної дошки з гробниці його імені, тримає в руках вимірювальні інструменти, в яких зафіксовані пропорції золотого розподілу.

Греки ж були майстерними геометрами. Навіть арифметиці навчали своїх дітей за допомогою геометричних фігур. Квадрат Піфагора і діагональ цього квадрата були підставою для побудови динамічних

прямокутників.

Платон (427 ... 347гг. До н.е.) також знав про золотий розподіл. Його діалог "Тімей" присвячений математичним і естетичним поглядам школи Піфагора і, в

Зокрема, питанням золотого розподілу.

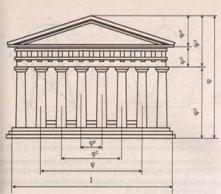
Парфенон має 8 колон по коротким сторонам і 17 по довгим. Відношення висоти будівлі до його довжини одно 0,618. Якщо зробити розподіл Парфенона по «золотого перерізу», то отримаємо ті чи інші виступи фасаду. При його розкопках виявлені циркулі, якими користувалися архітектори і скульптори античного світу. У помпейському циркулі (музей у Неаполі) також закладені пропорції золотого розподілу.

Рис.8. Парфенон

У дійшла до нас античній літературі золотий розподіл вперше згадується в "Засадах" Евкліда. У 2-ій книзі "Почав" дається геометрична побудова золотого розподілу. Після Евкліда дослідженням золотого розподілу займалися Гипсикл (II ст. До н.е.), Папп (III в. Н.е.) і ін .. У середньовічній Європі з золотим розподілом познайомилися по арабських перекладах "Почав" Евкліда. Перекладач Дж.Кампано з Наварри (III в.) Зробив до перекладу коментарі. Секрети золотого розподілу ревно оберігалися, зберігалися в суворій таємниці. Вони були відомі тільки обраним.

В епоху Відродження посилюється інтерес до золотого поділу серед вчених і художників у зв'язку з його застосуванням, як в геометрії, так і в мистецтві, особливо в архітектурі. Леонардо да Вінчі, художник і вчений, бачив, що в італійських художників великий емпіричний досвід, але недолік знань. Він задумав і почав писати книгу по геометрії, але в цей час з'явилася книга ченця Луки Пачолі, і Леонардо залишив свою витівку. На думку сучасників і істориків науки, Лука Пачолі був справжнім світилом, найбільшим математиком Італії в період між Фібоначчі і Галілеєм.

Лука Пачолі чудово розумів значення науки для мистецтва. У 1496 р на запрошення герцога Моро він приїжджає в Мілан, де читає лекції з математики. У Мілані при дворі Моро в той час працював і Леонардо да Вінчі. У 1509г. у Венеції була видана книга Луки Пачолі "Божественна пропорція" з блискуче виконаними ілюстраціями, через що вважають, що їх зробив Леонардо да Вінчі. Книга була захопленим гімном золотої пропорції. Серед багатьох достоїнств золотої пропорції чернець Лука Пачолі не забув назвати і її "божественну суть" як вираження божественної триєдності: бог син, бог батько і бог дух святий (малося на увазі, що малий відрізок є уособлення бога сина, більший відрізок - бога батька, а весь відрізок - бога духу святого).

Леонардо да Вінчі також багато уваги приділяв вивченню золотого розподілу. Він справляв перетину стереометричного тіла, утвореного правильними п'ятикутниками, і кожен раз отримував прямокутники з відносинами сторін у золотому розподілі. Тому він дав цьому розподілу назва золотий перетин. Так воно і тримається досі як найпопулярніше.

У той же час на півночі Європи, в Німеччині, над тими ж проблемами трудився Альбрехт Дюрер. Він робить начерки введення до першого варіанту трактату про пропорції. Дюрер пише: "Необхідно, щоб той, хто що-небудь уміє, навчив цього інших, які цього потребують. Це я і думав був учинити".

Судячи по одному з листів Дюрера, він зустрічався з Лукою Пачолі під час перебування в Італії. Альбрехт Дюрер докладно розробляє теорію пропорцій людського тіла. Важливе місце в своїй системі співвідношень Дюрер відводив золотому перетину. Зростання людини ділиться в золотих пропорціях лінією пояса, а також лінією, проведеною через кінчики середніх пальців опущених рук, нижня частина обличчя - ротом і т.д. Відомий пропорційний циркуль Дюрера.

Побудова ряду відрізків золотої пропорції можна робити як в сторону збільшення (зростаючий ряд), так і в бік зменшення (спадний ряд).

Якщо на прямий довільної довжини, відкласти відрізок m (φ), поруч відкладаємо відрізок M. На підставі цих двох відрізків вибудовуємо шкалу відрізків золотої пропорції висхідного і спадного рядів

У наступні століття правило золотої пропорції перетворилося в академічний канон і, коли з часом в мистецтві почалася боротьба з академічною рутиною, в запалі боротьби "разом з водою виплеснули і дитину". Знову "відкрито" золотий перетин було в середині XIX в. У 1855р. німецький дослідник золотого перетину професор Цейзинг опублікував свою працю "Естетичні дослідження". З Цейзинг сталося саме те, що і повинно було неминуче відбутися з дослідником, який розглядає явище як таке, без зв'язку з іншими явищами. Він абсолютизував пропорцію золотого перетину, оголосивши її універсальною для всіх явищ природи і мистецтва. У Цейзинга були численні послідовники, але були і противники, які оголосили його вчення про пропорції "математичною естетикою".

3. Побудова пропорції.

Тут наводиться побудову точки Е, який ділив відрізок прямої в пропорції золотий перетин.

Мал. 1. Розподіл відрізка прямої по золотому перетину. BC = 1/2 AB; CD = BC

З точки В відновлюється перпендикуляр, рівний половині АВ. Отримана точка С з'єднується лінією з точкою А. На отриманій лінії відкладається відрізок ВС, що закінчується точкою D. Відрізок AD переноситься на пряму АВ. Отримана при цьому точка Е ділить відрізок АВ у співвідношенні золотої пропорції.

Саме ці відрізки використовував Евклід при побудові правильного п'ятикутника, тому що кожна зі сторін п'ятикутної зірки ділиться іншими саме в такій пропорції.

Таким чином, зірчастий п'ятикутник також володіє «золотим перетином». Цікаво, що всередині п'ятикутника можна продовжити будувати п'ятикутники, і це ставлення буде зберігатися.

Зірчастий п'ятикутник називається пентаграммой. Піфагорійці вибрали п'ятикутну зірку в якості талісмана, вона вважалася символом здоров'я і служила розпізнавальним знаком.

В даний час існує гіпотеза, що пентаграма - первинне поняття, а «золотий перетин» вдруге. Пентаграмму ніхто не винаходив, її тільки скопіювали з натури. Вид п'ятикутної зірки мають п'яти-пелюсткові квіти плодових дерев і чагарників, морські зірки. Ті та інші створіння природи людина спостерігає вже тисячі років. Тому природно припустити, що геометричний образ цих об'єктів - пентаграма - стала відома раніше, ніж «золота» пропорція.

4.Другий золотий перетин.

Болгарський журнал «Вітчизна» (№10, 1983) опублікував статтю Цвєтана Цекова-Олівця «Про другий золотий перетин», яке випливає з основного перетину і дає інше ставлення 44: 56.

Така пропорція виявлена ​​в архітектурі, а також має місце при побудові композицій зображень подовженого горизонтального формату. <! DOCTYPE HTML PUBLIC "- // W3C // DTD HTML 4.0 Transitional // EN"> <! - saved from url = (0026) http://nt.ru/tp/iz/zs.htm -> <DIV align = center>

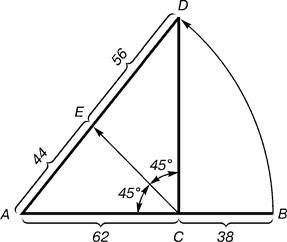
Розподіл здійснюється наступним чином. Відрізок АВ ділиться в пропорції золотого перетину. З точки С, підіймали перпендикуляр СD. Радіусом АВ знаходиться точка D, яка з'єднується лінією з точкою А. Прямий кут АСD ділиться навпіл. З точки З проводиться лінія до перетину з лінією AD. Точка Е ділить відрізок AD щодо 56:44.

Мал. 2. Побудова другого золотого перетину

На малюнку показано положення лінії другого золотого перетину. Вона знаходиться посередині між лінією золотого перетину і середньою лінією прямокутника.

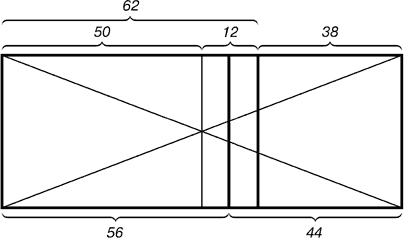
Мал. 3. Розподіл прямокутника лінією другого золотого перетину

Таким чином було доведено, що розділити відрізок в крайньому і середньому відношенні можна не єдиним способом.

5. "Золоті" фігури.

5.1.Золотой прямокутник:

Якщо побудувати квадрат зі стороною АВ = а, знайти середину М відрізка АВ і провести дугу кола радіусом МС з центром в точці М до перетину з продовженням боку АВ в точці Е, то точка В розділить відрізок АЕ в крайньому і середньому відношенні.

Щоб переконатися в цьому, зауважимо, що по теоремі Піфагора

МС2 = А2 + (а / 2) 2 = 5А2 / 4

В силу чого

АЕ = а / 2 + МЕ = (√5 + 1) а / 2 = φАВ

Прямокутник АЕ FD зі сторонами АЕ = φА D називається золотим прямокутником. Чотирикутник АВС D - квадрат. Неважко бачити, що прямокутник ВЕ F З також золотий, оскільки BC = a = φВЕ. Ця обставина відразу наводить на думку про подальше розбитті прямокутника ВЕ F С.

Чи можна вважати, що прямокутник з відношенням сторін, рівним φ, виглядає витонченіше, ніж прямокутники з відношенням сторін, скажімо, 2: 1, 3: 2 або 5: 7? Щоб відповісти на це питання, були проведені спеціальні експерименти. Результати їх не цілком переконливі, але все ж свідчать про деяке перевазі, що віддається золотого перетину. Втім, чи може прямокутник сам по собі бути захоплююче прекрасним або відштовхуюче потворним?

5.2.Золотой трикутник:

Проводимо пряму АВ. Від точки А

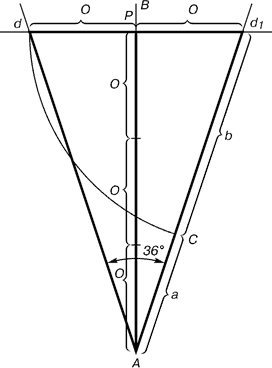відкладаємо на ній три рази відрізок О

довільної величини, через

отриману точку Р проводимо перпендикуляр до лінії

АВ, на перпендикуляре вправо і вліво від точки Р відкладаємо відрізки О. Отримані точки d і d1 з'єднуємо прямими з точкою А. Відрізок dd1

відкладаємо на лінію Ad1, отримуючи точку С. Вона розділила лінію Ad1 в пропорції золотого перетину. Лініями Ad1 і dd1 користуються для побудови «золотого»

прямокутника.

5.3. Золотий п'ятикутник; побудова Евкліда.

Чудовий приклад «золотого перетину» являє собою правильний п'ятикутник - опуклий і зірчастий (рис.5).

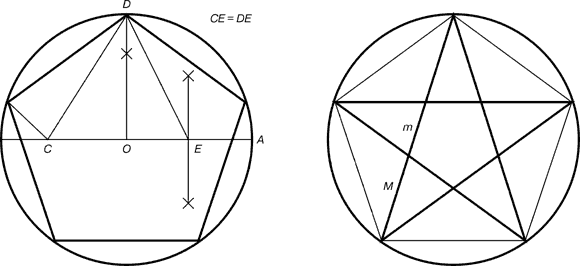
Рис.6. Побудова правильного п'ятикутника і пентаграми.

Для побудови пентаграми необхідно побудувати правильний п'ятикутник.

Нехай О - центр кола, А - точка на окружності і Е - середина відрізка ОА. Перпендикуляр до радіуса ОА, відновлений в точці О, перетинається з окружністю в точці D. Користуючись циркулем, відкладемо на діаметрі відрізок CE = ED. Довжина сторони вписаного в коло правильного п'ятикутника дорівнює DC. Відкладаємо на окружності відрізки DC і отримаємо п'ять точок для накреслення правильного п'ятикутника. З'єднуємо кути п'ятикутника через один діагоналями і отримуємо пентаграму. Все іагоналі п'ятикутника ділять один одного на відрізки, пов'язані між собою золотий пропорцією.

Кожен кінець п'ятикутної зірки являє собою золотий трикутник. Його сторони утворюють кут 36 ° при вершині, а підстава, відкладене на бічну сторону, ділить її в пропорції золотого перетину.

Є і золотий кубоід- це прямокутний паралелепіпед з ребрами, що мають довжини 1.618, 1 і 0.618.

Тепер розглянемо доказ, запропоноване Евклидом в «Засадах».

Подивимося тепер, як Евклід використовує золотий перетин для того, щоб побудувати кут в 72 градуси - саме під таким кутом видно сторона правильного п'ятикутника з центру описаного кола. Почнемо з відрізка АВЕ, розділеного в середньому і крайньому відношенні точкою В. Проведемо далі дуги кіл з центрами в точках В і Е і радіусах АВ, пересічні в точці С. Трохи нижче доведемо, що АС = АЕ, а поки приймемо це на віру.

Отже, нехай АС = АЕ. Позначимо через a рівні кути ЄВС і СЕВ. Так як АС = АЕ, то кут АСЕ також дорівнює a. Теорема про те, що сума кутів трикутника дорівнює 180 градусів, дозволяє знайти кут ВСЕ: він дорівнює 180-2 a, а кут ЕАС - 3 a - 180. Але тоді кут АВС дорівнює 180 a. Підсумовуючи кути трикутника АВС отримуємо,

180 = (3 a -180) + (3 a -180) + (180 - a)

Звідки 5 a = 360, значить a = 72.

Отже, кожен з кутів при основі трикутника ВЕС вдвічі більше кута при вершині, рівного 36 градусів. Отже, щоб побудувати правильний п'ятикутник, необхідно лише провести будь-яку окружність з центром в точці Е, що перетинає ЄС в точці Х і сторону ЕВ в точці Y: відрізок XY служить одній зі сторін вписаного в коло правильного п'ятикутника; Обійшовши навколо всьому колу, можна знайти і всі інші сторони.

Доведемо тепер, що АС = АЕ. Припустимо, що вершина З з'єднана відрізком прямої з серединою N відрізка ВЕ. Зауважимо, що оскільки СВ = РЄ, то кут З N Е прямий. По теоремі Піфагора:

CN 2 = А2 - (а / 2 j) 2 = а2 (1-4 j 2)

Звідси маємо (АС / а) 2 = (1 + 1/2 j) 2 + (1-1 / 4 j 2) = 2 + 1 / j = 1 + j = j 2

Отже, АС = j а = j АВ = АЕ, що й треба було довести

5.4.Спіраль Архімеда.

Послідовно відсікаючи від золотих прямокутників квадрати до нескінченності, кожен раз поєднуючи протилежні точки чвертю кола, ми отримаємо досить витончену криву. Першим увагу на неї звернув давньогрецький вчений Архімед, ім'я якого вона і носить. Він вивчав її і вивів рівняння цієї спіралі.

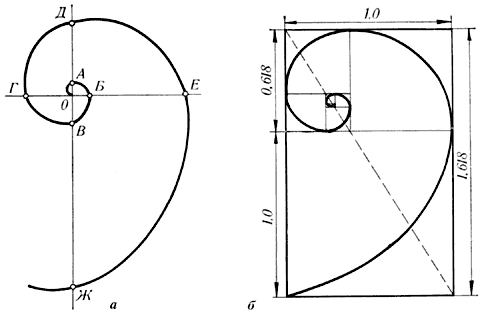
В даний час спіраль Архімеда широко використовується в техніці.

6.Чісла Фібоначчі.

З золотим перетином побічно пов'язане ім'я італійського математика Леонардо з Пізи, який відомий більше за своїм прізвисько Фібоначчі (Fibonacci - скорочена filius Bonacci, тобто син Боначчі)

У 1202г. їм була написана книга "Liber abacci", тобто "Книга про абаці". "Liber abacci" являє собою об'ємний працю, що містить майже всі арифметичні і алгебраїчні відомості того часу і зіграв помітну роль у розвитку математики в Західній Європі протягом кількох наступних століть. Зокрема, саме по цій книзі європейці познайомилися з індуськими ( "арабськими") цифрами.

Який посилає в книзі матеріал пояснюється на великому числі завдань, які становлять значну частину цього трактату.

Розглянемо одну таку задачу:

"Скільки пар кроликів в один рік від однієї пари народжується?

Хтось помістив пару кроликів в якомусь місці, обгородженому з усіх боків стіною, щоб дізнатися, скільки пар кроликів народиться протягом цього року, якщо природа кроликів така, що через місяць пара кроликів відтворить іншу, а народжують кролики з другого місяця після свого народження "

місяці

1

2

3

4

5

6

7

8

9

10

11

12

пари кроликів

2

3

5

8

13

21

34

55

89

144

233

377

Табл.1 Ряд Фібоначчі при u1 = 1

Перейдемо тепер від кроликів до чисел і розглянемо наступну числову послідовність:

u 1, u 2 ... un

в якій кожен член дорівнює сумі двох попередніх, тобто при всякому n> 2

un = un-1 + un-2.

Дана послідовність асимптотично (наближаючись все повільніше і повільніше) прагне до деякого постійного співвідношенню. Однак, це співвідношення ірраціонально, тобто являє собою число з нескінченної, непередбачуваною послідовністю десяткових цифр у дробовій частині. Його неможливо виразити точно.

Якщо який-небудь член послідовності Фібоначчі розділити на попередній йому (наприклад, 13: 8), результатом буде величина, що коливається близько ірраціонального значення 1.61803398875 ... і через раз то перевершує, то що не досягає його.

Асимптотична поведінка послідовності, затухаючі коливання її співвідношення близько ірраціонального числа Ф можуть стати більш зрозумілими, якщо показати відносини декількох пеpвая членів послідовності. У цьому прикладі наведено відносини другого члена до першого, третього до другого, четвертого до третього, і так далі:

1: 1 = 1.0000, що менше фі на 0.6180

2: 1 = 2.0000, що більше фі на 0.3820

3: 2 = 1.5000, що менше фі на 0.1180

5: 3 = 1.6667, що більше фі на 0.0486

8: 5 = 1.6000, що менше фі на 0.0180

У міру просування по суммационной послідовності Фібоначчі кожен новий член ділитиме наступний зі все більшим і більшим наближенням до недосяжного Ф.

Людина підсвідомо шукає Божественну пропорцію: вона потрібна для задоволення його потреби в комфорті.

Пpи розподілі будь-якого члена послідовності Фібоначчі на наступний за ним виходить просто зворотна до 1.618 величина (1: 1.618 = 0.618). Але це теж досить незвичайне, навіть чудове явище. Оскільки пеpвоначально співвідношення - нескінченна дpобь, у цього співвідношення також не повинно бути кінця.

При розподілі кожного числа на наступне за ним через одне, отримуємо число 0.382

1: 0.382 = 2.618

Підбираючи таким чином співвідношення, отримуємо основний набір коефіцієнтів Фібоначчі: 4.235, 2.618, 1.618,0.618,0.382,0.236.Упомянем також 0.5.Все вони відіграють особливу роль в природі і зокрема в технічному аналізі.

Тут необхідно зазначити, що Фібоначчі лише нагадав свою послідовність людству, так як вона була відома ще в стародавні часи під назвою Золотий перетин.

Золотий перетин, як ми бачили, виникає в зв'язку з правильним п'ятикутником, тому і числа Фібоначчі грають роль у всьому, що має відношення до правильного п'ятикутника - опуклим і зірчастим.

Ряд Фібоначчі міг би залишитися тільки математичним казусом, якби не та обставина, що всі дослідники золотого поділу в рослинному і в тваринному світі, не кажучи вже про мистецтво, незмінно приходили до цього ряду як арифметичному вираженню закону золотого перерізу. Вчені продовжували активно розвивати теорію чисел Фібоначчі і золотого перетину. Ю. Матіясевіч з використанням чисел Фібоначчі вирішує 10-ю проблему Гільберта (про рішення Діофантових рівнянь). Виникають витончені методи вирішення ряду кібернетичних задач (теорії пошуку, ігор, програмування) з використанням чисел Фібоначчі і золотого перетину. У США створюється навіть Математична Фібоначчі-асоціація, яка з 1963 року випускає спеціальний журнал.

Одним з досягнень в цій області є відкриття узагальнених чисел Фібоначчі і узагальнених золотих перетинів. Ряд Фібоначчі (1, 1, 2, 3, 5, 8) і відкритий ним же «двійковий» ряд чисел 1, 2, 4, 8, 16 ... (тобто ряд чисел до n, де будь-яке натуральне число, менше n можна представити сумою деяких чисел цього ряду) на перший погляд абсолютно різні. Але алгоритми їх побудови досить схожі один на одного: в першому випадку кожне число є сума попереднього числа з самим собою 2 = 1 + 1; 4 = 2 + 2 ..., у другому - це сума двох попередніх чисел 2 = 1 + 1, 3 = 2 + 1, 5 = 3 + 2 .... Чи не можна відшукати загальну математичну формулу, з якої виходять і « двійковий »ряд, і ряд Фібоначчі?

Дійсно, задамося числовим параметром S, який може приймати будь-які значення: 0, 1, 2, 3, 4, 5 ... Розглянемо числовий ряд, S + 1 перших членів якого - одиниці, а кожен з наступних дорівнює сумі двох членів попереднього і віддаленого від попереднього на S кроків. Якщо n-й член цього ряду ми позначимо через S (n), то отримаємо загальну формулу S (n) = S (n - 1) + S (n - S - 1).

Очевидно, що при S = ​​0 з цієї формули ми одержимо «двійковий» ряд, при S = ​​1 -ряд Фібоначчі, при S = ​​2, 3, 4. нові ряди чисел, які отримали назву S-чисел Фібоначчі.

У загальному вигляді золота S-пропорція є позитивний корінь рівняння золотого S-перетину xS + 1 - xS - 1 = 0.

Неважко показати, що при S = ​​0 виходить розподіл відрізка навпіл, а при S = ​​1 - знайоме класичне золотий перетин.

Відносини сусідніх S-чисел Фібоначчі з абсолютною математичною точністю збігаються в межі з золотими S-пропорціями! Тобто золоті S-перетину є числовими інваріантами S-чисел Фібоначчі.

7.Золотое перетин в мистецтві.

7.1. Золотий перетин в живопису.

Переходячи до прикладів «золотого перетину» в живописі, не можна не зупинити своєї уваги на творчості Леонардо да Вінчі. Його особистість - одна із загадок історії. Сам Леонардо да Вінчі говорив: «Нехай ніхто, не будучи математиком, чи не наважиться читати мої труди».

Немає сумнівів, що Леонардо да Вінчі був великим художником, це визнавали вже його сучасники, але його особистість і діяльність залишаться покритими таємницею, так як він залишив нащадкам не зв'язний виклад своїх ідей, а лише численні рукописні начерки, замітки, в яких йдеться «про все на світі ».

Портрет Мони Лізи (Джоконди) довгі роки привертає увагу дослідників, які виявили, що композиція малюнка заснована на золотих трикутниках, які є частинами правильного зірчастого п'ятикутника ..

Також пропорція золотого перетину проявляється в картині Шишкіна. На цій знаменитій картині І. І. Шишкіна з очевидністю проглядаються мотиви золотого перетину. Яскраво освітлена сонцем сосна (що стоїть на першому плані) ділить довжину картини по золотому перетину. Праворуч від сосни - освітлений сонцем пагорб. Він ділить по золотому перетину праву частину картини по горизонталі.

У картині Рафаеля "Побиття немовлят" проглядається інший елемент золотий пропорції - золота спіраль. На підготовчому ескізі Рафаеля проведені червоні лінії, що йдуть від смислового центру композиції - точки, де пальці воїна зімкнулися навколо щиколотки дитини - уздовж фігур дитини, жінки, що притискає його до себе, воїна з занесеним мечем і потім уздовж фігур такої ж групи в правій частині ескізу . Невідомо, будував чи Рафаель золоту спіраль або відчував її.

Т.Кук використовував при аналізі картини Сандро Боттічеллі «народження Венери» золоте сеченеіе.

7.2. Піраміди золотого перетину.

Широко відомі медичні властивості пірамід, особливо золотого перетину. За деякими найбільш поширеним думкам, кімната, в якій знаходиться така піраміда, здається більше, а повітря - прозоріше. Сни починають запам'ятовуватися краще. Також відомо, що золотий перетин широко застосовувалася в архітектурі і скульптурі. Прикладом тому стали: Пантеон і Парфенон в Греції, будівлі архітекторів Баженова і Малевича

8. Висновок.

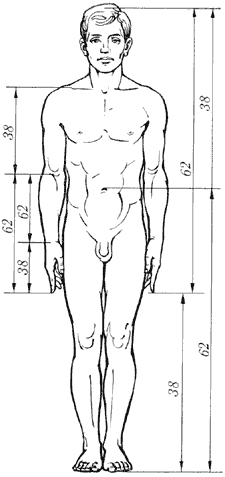Необхідно сказати, що золотий перетин має велике застосування в нашому житті.

Було доведено, що людське тіло ділиться в пропорції золотого перетину лінією пояса.

Раковина наутилуса закручена подібно золотий спіралі.

Завдяки золотого перетину був відкритий пояс астероїдів між Марсом і Юпітером - по пропорції там повинна знаходитися ще одна планета.

Порушення струни в точці, що ділить її у відношенні золотого поділу, не викличе коливань струни, тобто це точка компенсації.

На літальних апаратах з електромагнітними джерелами енергії створюються прямокутні осередки з пропорцією золотого перетину.

Джоконда побудована на золотих трикутниках, золота спіраль присутня на картині Рафаеля «Побиття немовлят».

Пропорція виявлена ​​в картині Сандро Боттічеллі «Народження Венери»

Відомо багато пам'ятників архітектури, побудованих з використанням золотої пропорції, в тому числі Пантеон і Парфенон в Афінах, будівлі архітекторів Баженова і Малевича.

Іоанну Кеплеру, що жив п'ять століть тому, належить вислів: "Геометрія володіє двома великими скарбами. Перше - це теорема Піфагора, друге - ділення відрізка в крайньому і середньому відношенні"

список літератури

1. Д. Пидоу. Геометрія і мистецтво. - М .: Мир, 1979.
2. Журнал "Наука і техніка"

3. Журнал «Квант», 1973, № 8.
4. Журнал «Математика в школі», 1994, № 2; № 3.

5. Ковальов Ф.В. Золотий перетин в живопису. К .: Вища школа, 1989.

6. Стахов А. Коди золотої пропорції.

7.Воробьев М.М. "Числа Фібоначчі" - М .: Наука 1964

8. "Математика - Енциклопедія для дітей" М .: Аванта +, 1998.

9. Інформація з інтернету.

Для подготовки даної роботи були вікорістані матеріали з сайту http://www.ed.vseved.ru/

Дата додавання: 04.03.2003