випромінювання

Наша взаимовыгодная связь https://banwar.org/

Випромінювань е ня електромагнітне, процес утворення вільного електромагнітного поля. (Термін «І.» застосовують також для позначення самого вільного, т. Е. Излученного, електромагнітного поля - см. Максвелла рівняння , Електромагнітні хвилі .) Класична фізика розглядає І. як випускання електромагнітних хвиль прискорено рухомими електричними зарядами (зокрема, змінними струмами). Класична теорія пояснила дуже багато характерних рис процесів І., проте вона не змогла дати задовільного опису ряду явищ, особливо теплового випромінювання тел і І. мікросистем (атомів і молекул). Такий опис виявилося можливим лише в рамках квантової теорії І., яка показала, що І. є народження фотонів при зміні стану квантових систем (наприклад, атомів). Квантова теорія, більш глибоко проникнувши в природу І., одночасно вказала і межі застосування класичної теорії: остання часто є дуже хорошим наближенням при описі І., залишаючись, наприклад, теоретичною базою радіотехніки (див. Випромінювання і прийом радіохвиль ).

Класична теорія випромінювання (теорія Максвелла). Фізичні причини існування вільного електромагнітного поля (т. Е. Поля самопідтримки, незалежного від порушили його джерел) тісно пов'язані з тим, що електромагнітні хвилі поширюються від джерел - зарядів і струмів - не миттєво, а з кінцевою швидкістю c (в вакуумі c @ 3 • 1010 см / сек). Якщо джерело І. (наприклад, змінний струм) в якийсь момент зникне, це не призведе до миттєвого зникнення поля у всьому просторі: у віддалених від джерела точках воно зникне лише через кінцевий проміжок часу. З теорії Максвелла випливає, що зміна в часі електричного поля Е породжує магнітне поле Н, а зміна Н - вихровий електричне поле. Звідси випливає, що самопідтримується може бути лише змінне електромагнітне поле, в якому обидві його компоненти - Е і Н, безперервно змінюючись, постійно порушують одна іншу.

В процесі І. електромагнітне поле забирає від джерела енергію. Щільність потоку енергії цього поля (кількість енергії, що протікає за одиницю часу через одиничну площадку, орієнтовану перпендикулярно напрямку потоку) визначається Пойнтинга вектором П, який пропорційний векторному добутку [ЕН].

Інтенсивність І. E изл є енергія, що буря полем від джерела в одиницю часу. Порядок її величини можна оцінити, обчисливши твір площі замкнутої поверхні, що охоплює джерело на середнє значення абсолютної величини щільності потоку П на цій поверхні (П ~ EH). Зазвичай поверхню вибирають у формі сфери радіусу R (її площа ~ R) і обчислюють E изл в межі R ® ¥:

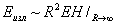(1)

(Е і Н - абсолютні величини векторів Е і Н).

Для того щоб ця величина не зверталася в нуль, т. Е. Щоб вдалині від джерела існувало вільне електромагнітне поле, необхідно, щоб і Е, і Н убували не швидше, ніж 1 / R. Ця вимога задовольняється, якщо джерелами полів є прискорено рухомі заряди. Поблизу від зарядів підлогу я - кулонівських, пропорційні 1 / R 2, але на великих відстанях основну роль починають грати некулоновскіе поля Е і Н, що мають закон убування 1 / R.

І. рухомого заряду. Найпростішим джерелом поля є точковий заряд. У покоїться заряду І. відсутня. Рівномірно рухається заряд (в порожнечі) також не може бути джерелом І. Заряд ж, що рухається прискорено, випромінює. Прямі обчислення на основі рівнянь Максвелла показують, що інтенсивність його І. дорівнює

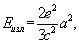(2)

де е - величина заряду, a - його прискорення. (Тут і нижче використовується Гауссова система одиниць, см. СГС система одиниць .) В залежності від фізичної природи прискорення І. інколи набуває особливих найменування. Так, І., що виникає при гальмуванні заряджених частинок в речовині в результаті впливу на них кулонівських полів ядер і електронів атомів, називається гальмівним випромінюванням . І. зарядженої частинки, що рухається в магнітному полі, викривляється її траєкторію, називається синхротронним випромінюванням (Або магнітотормозного І.). Воно спостерігається, наприклад, в циклічних прискорювачах заряджених частинок .

В окремому випадку, коли заряд здійснює гармонійне коливання, прискорення а за величиною дорівнює добутку відхилення заряду від положення рівноваги (х = x 0 sin w t, x 0 - амплітуда відхилення х) на квадрат частоти w. Усереднена за часом t інтенсивність І.

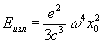(3)

дуже швидко (пропорційно w 4) зростає при збільшенні частоти.

Електричне дипольне І. Найпростішою системою, яка може бути джерелом І., є два пов'язаних один з одним, хто вагається, рівних за величиною, різнойменних заряду. вони утворюють диполь зі змінним моментом. Якщо, наприклад, заряди диполя здійснюють гармонійні коливання назустріч один одному, то дипольний електричний момент змінюється за законом d = d 0 sin w t (w - частота коливань, d 0 - амплітуда моменту d). Усереднена за часом t інтенсивність І. такого диполя

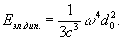(4)

І., розходиться від коливного диполя, неізотропно, т. Е. Енергія, що випускається їм в різних напрямках, неоднакова. Уздовж осі коливань І. взагалі відсутня. Під прямим же кутом до осі коливань І. максимально. Для всіх проміжних напрямків кутовий розподіл І. змінюється пропорційно sin2 J, де кут J відлічується від напрямку осі коливань. Якщо напрямок осі коливань диполя змінюється з часом, то усереднене кутовий розподіл стає більш складним.

Реальні випромінювачі, як правило, включають безліч зарядів. Точний облік всіх деталей руху кожного з них при дослідженні І. зайвий (а часто і неможливий). Дійсно, І. визначається значеннями полів далеко від джерела, т. Е. Там, де деталі розподілу зарядів (і струмів) у випромінювачі позначаються слабо. Це дозволяє замінювати дійсний розподіл зарядів наближеним. Найгрубішим, «нульовим» наближенням є розгляд випромінюючої системи як одного заряду, за величиною дорівнює сумі зарядів системи. У електронейтральної системи, сума зарядів якої дорівнює нулю, І. в цьому наближенні відсутній. У наступному, першому, наближенні позитивні і негативні заряди системи окремо подумки «стягуються» до центрів свого розподілу. Для електронейтральної системи це означає уявну заміну її електричним диполем, що випромінюють згідно (4). Таке наближення називається дипольним, а відповідне І. - електричним дипольним І.

Електричне квадрупольному і вищі мультипольні І. Якщо у системи зарядів дипольне І. відсутня, наприклад через рівності дипольного моменту нулю, то необхідно враховувати наступне наближення, в якому система зарядів - джерело І. - розглядається як квадруполь , Т. Е. Чотириполюсник. Найпростіший квадруполь - 2 диполя, які мають рівні за величиною і протилежні по напрямку моменти. Ще більш детальний опис випромінюючої системи зарядів дає розгляд наступних наближень, в яких розподіл зарядів описується мультиполя (Багатополюсника) вищих порядків (диполь називається мультиполя 1-го, квадруполь - 2-го і т. Д. Порядків).

Важливо відзначити, що в кожному наступному наближенні інтенсивність І. приблизно в (v / c) 2 менше, ніж в попередньому (якщо, звичайно, останнє не відсутній з яких-небудь причин). Якщо випромінювач - нерелятивістський, т. Е. Все заряди мають швидкості, багато менші, ніж світлова (v / c << 1), то головну роль відіграє нижче незникаюче наближення. Так, якщо є дипольне І., воно є основним, а всі інші вищі мультипольні поправки вкрай малі і їх можна не враховувати. У разі ж І. релятивістських частинок опис І. за допомогою мультиполів стає неефективним, так як внесок мультиполів вищих порядків перестає бути малим.

Магнітне дипольне І. Крім електричних диполів і вищих мультиполів, джерелами І. можуть бути також магнітні диполі і мультиполя (як правило, основним є дипольне магнітне І.). Картина розподілу магнітного поля на великих відстанях від контуру, по якому протікає струм, який породжує це поле, подібна картині розподілу електричного поля далеко від електричного диполя. Аналог дипольного електричного моменту - дипольний магнітний момент М - визначається силою струму I в контурі і його геометрією. Для плоского контуру абсолютна величина моменту М = (e / c) IS, де S - площа, що охоплюється контуром. Формули для інтенсивності магнітного дипольного І. майже такі ж, як і для електричного, тільки замість електричного дипольного моменту d в них коштує магнітний момент М. Так, якщо магнітний момент змінюється за гармонійним законом М = M 0 sin w t (для цього повинна гармонійно змінюватися сила струму I в контурі), то усереднена за часом інтенсивність І. дорівнює:

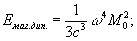(5)

тут M 0 - амплітуда магнітного моменту M.

Ставлення магнітного дипольного моменту до електричного має порядок v / c, де v - швидкість руху зарядів, що утворюють струм; звідси випливає, що інтенсивність магнітного дипольного І. в (v / c) 2 разів менше, ніж дипольного електричного, якщо, звичайно, останнім присутній. Таким чином, інтенсивності магнітного дипольного і електричного квадрупольного І. мають однаковий порядок величини.

І. релятивістських частинок. Одним з найважливіших прикладів такого І. є синхротронное І. заряджених частинок в циклічних (кільцевих) прискорювачах. Різка відмінність від нерелятівістского І. проявляється тут вже в спектральному складі І .: якщо частота звернення зарядженої частинки в прискорювачі дорівнює w (нерелятивістський випромінювач випускав би хвилі такої ж частоти), то інтенсивність її І. має максимум при частоті w макс ~ g3 w, де g = [1 - (v / c) 2] -1/2, т. е. основна частка І. при v ® з доводиться на частоти, вищі, ніж w. Таке І. направлено майже по дотичній до орбіти частинки, в основному вперед у напрямку її руху.

Ультрарелятивістських частка може випромінювати електромагнітні хвилі, навіть якщо вона рухається прямолінійно і рівномірно (але тільки в речовині, а не в порожнечі!). Це І., назване Черенкова - Вавилова випромінюванням , Виникає, якщо швидкість зарядженої частинки в середовищі перевершує фазову швидкість світла в цьому середовищі (u фаз = c / n, де n - показник заломлення середовища). І. з'являється через те, що частка «переганяє» породжується нею поле, відривається від нього.

Квантова теорія випромінювання. Вище вже говорилося, що класична теорія дає лише наближене опис процесів І. (весь фізичний світ в принципі є «квантовим»). Однак існують і такі фізичні системи, І. яких неможливо навіть приблизно описати в згоді з досвідом, залишаючись на позиціях класичної теорії. Важлива особливість таких квантових систем, як атом або молекула, полягає в тому, що їх внутрішня енергія не змінюється безперервно, а може приймати лише певні значення, що утворюють дискретний набір. Перехід системи зі стану з однією енергією в стан з іншого енергією (див. квантові переходи ) Відбувається стрибкоподібно; в силу закону збереження енергії система при такому переході повинна втрачати або здобувати певну «порцію» енергії. Найчастіше цей процес реалізується у вигляді випускання (або поглинання) системою кванта І. - фотона . Енергія кванта e g = ћ w, де ћ - планка постійна (Ћ = 1,05450 × 10-27 ерг × сек), w - кругова частота. Фотон завжди виступає як єдине ціле, випускається і поглинається «повністю», в одному акті, має певну енергію, імпульс і спин (проекцію моменту кількості руху на напрям імпульсу), т. Е. Має низку корпускулярних властивостей. У той же час фотон різко відрізняється від звичайних класичних частинок тим, що у нього є і хвильові риси. Така подвійність фотона є частковий вияв корпускулярно-хвильового дуалізму .

Послідовної квантової теорії І. є квантова електродинаміка (див. Квантова теорія поля ). Однак багато результати, які стосуються процесам І. квантових систем, можна отримати з більш простий Напівкласична теорії І. Формули останньої, згідно відповідності принципу , При певному граничному переході повинні давати результати класичної теорії. Таким чином, встановлюється глибока аналогія між величинами, що характеризують процеси І. в квантової і класичної теорії.

І. атома. Система з ядра і рухається в його кулонівському полі електрона повинна знаходитися в одному з дискретних станів (на певному рівні енергії). При цьому їхні капітали, крім основного (т. Е. Має найменшу енергію), нестійкі. Атом, що перебуває в нестійкому (збудженому) стані, навіть якщо він ізольований, переходить в стан з меншою енергією. Цей квантовий перехід супроводжується випусканням фотона; таке І. називається спонтанним (мимовільним). Енергія, що буря фотоном e g = ћ w, дорівнює різниці енергії початкового i і кінцевого j станів атома (e i> e j, e g = e i - e j); звідси випливає формула Н. Бора для частот І .:

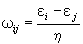(6)

Важливо відзначити, що такі характеристики спонтанного І., як напрям поширення (для сукупності атомів - кутовий розподіл їх спонтанного І.) і поляризація, що не залежать від І. інших об'єктів (зовнішнього електромагнітного поля).

Формула Бора (6) визначає дискретний набір частот (і отже, довжин хвиль) І. атома. Вона пояснює, чому спектри І. атомів мають добре відомий «лінійчатий» характер - кожна лінія спектра відповідає одному з квантових переходів атомів даної речовини.

Інтенсивність І. У квантовій теорії, як і в класичній, можна розглядати електричні дипольне і вищі мультипольні І. Якщо випромінювач нерелятивістський, основним є електричне дипольне І., інтенсивність якого визначається формулою, близькою до класичної:

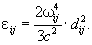(7)

Величини dij, є квантовим аналогом електричного дипольного моменту, виявляються відмінними від нуля лише при певних співвідношеннях між квантовими числами початкового i і кінцевого j станів (правила відбору для дипольного І.). Квантові переходи, що задовольняють таким правилам відбору, називаються дозволеними (фактично мається на увазі дозволене електричне дипольне І.). Переходи ж вищих мультипольного називаються забороненими. Ця заборона відносний: заборонені переходи мають відносно малу ймовірність, т. Е., Що відповідає ним інтенсивність І. невелика. Ті стану, переходи з яких «заборонені», є порівняно стійкими (довгоживучими). Вони називаються метастабільними станами .

Квантова теорія І. дозволяє пояснити не тільки відмінність в інтенсивності різних ліній, а й розподіл інтенсивності в межах кожної лінії; зокрема, ширину спектральних ліній .

Джерелами електромагнітного І. можуть бути не тільки атоми, але і більш складні квантові системи. Загальні методи опису І. таких систем ті ж, що і при розгляді атомів, але конкретні особливості І. вельми різноманітні. І. молекул, наприклад, має більш складні спектри, ніж І. атомів. Для І. атомних ядер типово, що енергія окремих квантів зазвичай велика (g-кванти), інтенсивність ж І. порівняно низька (див. Гамма-випромінювання , ядро атомне ).

Електромагнітне І. часто виникає і при взаємних перетвореннях елементарних частинок (анігіляції електронів і позитронів, розпаді нейтрального пі-мезона і т.д.).

Вимушене І. Якщо частота зовнішнього І., падаючого на вже збуджений атом, збігається з однією з частот можливих для цього атома згідно (6) квантових переходів, то атом випускає квант І., в точності такий же, як і налетів на нього (резонансний ) фотон. Це І. називається вимушеним. За своїми властивостями воно різко відрізняється від спонтанного - не тільки частота, але і напрямок поширення, і поляризація випущеного фотона виявляються тими ж, що у резонансного. Імовірність вимушеного І. (на відміну від спонтанного!) Пропорційна інтенсивності зовнішнього І., т. Е. Кількістю резонансних фотонів. Існування вимушеного І. було постулировано А. Ейнштейном при теоретичному аналізі процесів теплового І. тел з позицій квантової теорії і потім було підтверджено експериментально. У звичайних умовах інтенсивність вимушеного І. мала в порівнянні з інтенсивністю спонтанного. Однак вона сильно зростає в речовині, в якому в метастабільних станів знаходиться більше атомів, ніж в одному з станів з меншою енергією (в яке можливий квантовий перехід). При попаданні в таку речовину резонансного фотона випускаються фотони, в свою чергу відіграють роль резонансних. Число випромінюваних фотонів лавиноподібно зростає; результуюче І. складається з фотонів, абсолютно ідентичних за своїми властивостями, і утворює когерентний потік (див. когерентність ). На цьому явищі заснована дія квантових генераторів і квантових підсилювачів І.

Роль Теорії випромінювання. Практичне и науково-прикладне значення Теорії І. Величезна. На ній грунтується розробка и! Застосування лазерів и мазерів , Створення Нових джерел світла, ряд важлівіх досягнені в області радіотехнікі и спектроскопії. Розуміння і вивчення законів І. важливо і в іншому відношенні: за характером І. (енергетичному спектру, кутовому розподілу, поляризації) можна судити про властивості випромінювача. І. - поки фактично єдиний і дуже багатосторонній джерело інформації про космічні об'єкти. Наприклад, аналіз І., що приходить з космосу, привів до відкриття таких незвичайних небесних тіл, як пульсари . Вивчення спектрів далеких позагалактичних об'єктів підтвердило теорію розширюється Всесвіту . Одночасно вивчення І. дозволяє проникнути в область явищ мікросвіту. Саме теорії І. відіграють особливу роль у формуванні всієї сучасної фізичної картини світу: подолання труднощів, що виникли в електродинаміки рухомих середовищ, привело до створення відносності Теорії ; дослідження М. планка , присвячені теплового випромінювання , Поклали початок квантової теорії і квантовій механіці . Подальший розвиток теорії І. повинно привести до ще глибшого пізнання матерії.

Літ .: Тамм І. Е., Основи теорії електрики, 7 видавництво., М., 1957; Іваненко Д., Соколов А., Класична теорія поля, М. - Л., 1949; їх же, Квантова теорія поля, М. - Л., 1952; Ахиезер А. І., Берестецький В. Б., Квантова електродинаміка, 2 вид., М., 1959; Ландау Л. Д., Ліфшиц Е. М., Теорія поля, 5 видавництво., М., 1967 (Теоретична фізика, т. 2).

В. І. Григор'єв.